題目:0-1背包問題 (0-1 Knapsack Problem)
一個小偷在商店發現了數種不同的物品,每種物品僅各有一件,並分別有其重量與價值,小偷帶了一個背包,試圖藉由選取物品以獲取最大的價值,但背包有最大的承載量之限制。由於每件物品都不可分割,因此若背包添加一個物品後超過了最大承載量,則該物品必須被捨棄 ( 亦即,每件物品僅能不取或取,此謂之 0-1 )。試設計一個程式,計算其可獲取的最大價值之金額。
$w$:背包的承載量,單位為磅(pound),最大的承載量為磅。$n$:物品的總數量。
$w_{i}$:代表編號第 i 件物品的重量,單位為磅。
$v_{i}$:代表編號第 i 件物品的價值,單位為元(dollar)。
- 獲取的最大價值的遞迴式 (recurrence) 如下:
- 若 0 或 $w$ = 0 時,總價值 $c[ i,w ] = c[ 0 , x ] = c[ x , 0 ]$。
- 若 $w_i$ > $w$ 時,總價值 $c[ i , w ] = c[ i-1 , w ]$。
- 若 $i > 0$ 及 $w ≥ w_i$ 時,總價值 $c[ i , w ] = max(v_i+c[ i-1 , w - w_i],c[i-1,w]$)。 (例如, $max(a,b)$,即從 $a$ 與 $b$ 兩數中取其最大者)
- 本程式必須以動態規劃 (dynamic programming) 的方法解答。亦即,把一個大問分成多個子問題,先計算各子問題的答案並儲存起來,再結合子問題的答案來計算出此大問題的答案。
- 以二維矩陣的方式,逐漸地增加物品的編號及背包的承載量 $w$,計算並儲存 $c[i,w]$的數值。
- 每件物品的重量與背包的承載量都可被 10 整除。(例如,10, 20, 30, … 等)
- 背包的最大承載量:$w = 50$。
- 物品的總數量:$n = 3$。
- 各物品的重量與價值: $w_1 = 20$ , $v_1 = 100$ , $w_2 = 10$ , $v_2 = 60$; $w_1 = 30$ , $v_1 = 120$。
輸出說明:
- 以二維矩陣呈現不同的 $i$ 及 $w$ 值之背包內物品的總價值 $c[i,w]$,其中 $c[n,w]$ 即為獲取的最大價值之金額。
- 輸出格式範例: $c[ 0 \dots n , 0 \dots w]$,其中物品的編號 $i$ 為 0, 1, 2, 3,承載量 $w$ 為 0, 10, 20, 30, 40, 50。 0 0 0 0 0 0
0 x x x x x
0 x x x x x
0 x x x x x
因為題意不夠明確,在不影響題目情況下及方便 judge 系統比對答案,略作補充。
補充資料:
- 第一列輸入背包的最大承載量:$w$。($1\le w\le 10^4$)
- 第二列輸入物品的總數量:$n$。($1\le n\le 100$)
- 第三列輸入 $n$ 個物品重量 $w_i$,每個數值以空白隔開。$1\le w_i\le 100$
- 第四列輸入 $n$ 個物品價值 $v_i$,每個數值以空白隔開。$1\le v_i\le 100$
- 為了對齊方便,輸出格式如下說明:
- 根據 $c[i,w]$ 找出最長位數,以此位數為輸出長度,不足位數前補空白。
- 每個資料間以一個空白隔開。
- 最後一列需列出最大總價值為何?
範例一
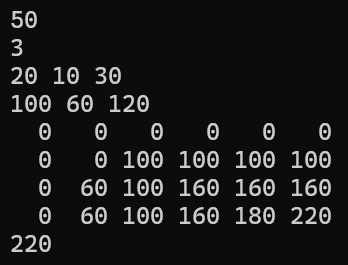
範例二
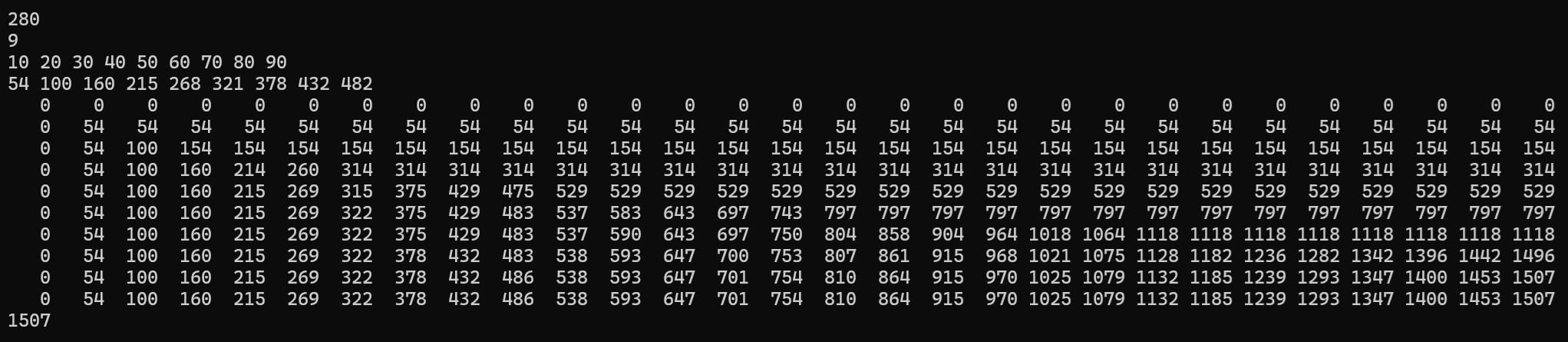
程式碼下載