- 九宮格魔方陣 有一名知名小說作者
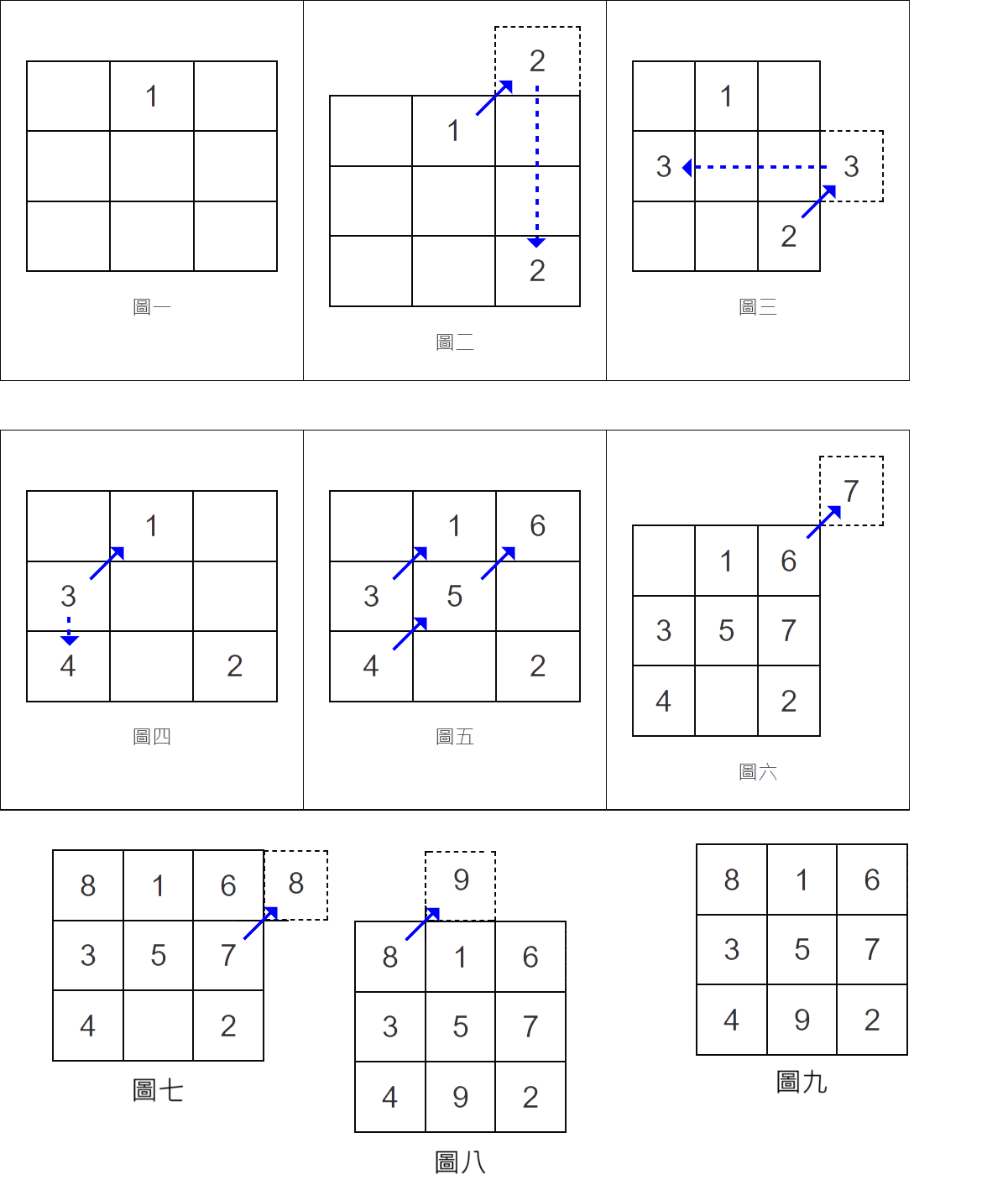
- 第一個數字放在第一行第一列的中央,如圖一。
- 數字加 1,而後向右上填數字:
- 如果填數字的格子在第一列的上方,則該數字向下沉底,如圖二、圖八。(圓形環繞上下連接)
- 如果填數字的格子在第三行的右方,則該數字向左沉底,如圖三、圖七。(圓形環繞左右連接)
- 如果填數字的格子已有數字,則該數字向下一格填入,如圖四。
- 如果填數字的格子是空的,則該數字直接填入,如圖五。
- 如果填數字的格子在第一列的上方以及第三行的右方,則該數字向下一格填入,如圖六。(圓形環繞上下左右連接)
- $3 \times 3$ 魔方陣完整的解題結果如圖九,我們可發現各行、各列與各對角線的和均為 15。
- 初始化九宮格
- 建立一個 $3\times 3$ 的空陣列 $magicSquare$,所有格子初始化為 0。
- 設定初始位置
- 第一個數字(1)放置在第一列的中間位置,$(row,col) = (0,1)$。 (註:$row = y, col = x$)
- 逐步填數字
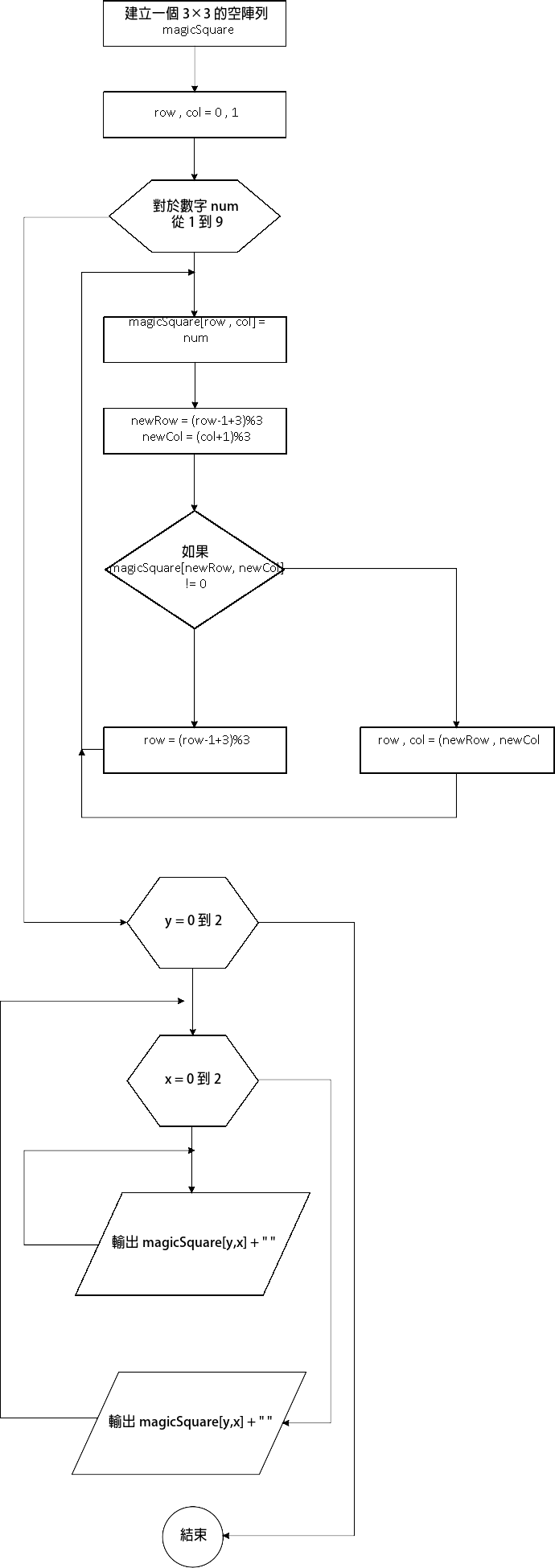
- 對於數字 $num$ 從 1 到 9:。
- 填入 $num$ 到 $magicSquare[row,col]$
- 新的一格 ($newRow , newCol$) = (($row$-1+3)%3,($col$+1)%3)
- 如果新的一格 ($newRow , newCol$) 已經有數字: $row$ = ($row$-1+3)%3
- 輸出結果
- 對於數數字 $y$ = 0 到 2
- 對於數數字 $x$ = 0 到 2
- 輸出 $magicSquare[row,col]$ 及一個空白
- 輸出跳行。
- 九宮格旋轉 如圖十,請將九宮資料順時針旋轉 90 度。(可參考 113 年工科技藝競賽第三題:魔方陣)
- 輸入資料
- 輸入 3 個數字,並以空白隔開。
- 以空白為分割,將三個資料放到矩陣 $matrix[y]$
- 選轉資料並輸出
- 令數字 y 從 0 到 2:。
- 令數字 x 從 0 到 2:。
- 輸出矩陣 $matrix[2-x,y]$ 加空白
- 輸出跳行
- 求 $e$ 在科學界,無論是力學或電學...,有個非常重要的常數叫
- 初始化
- 設定常數 $e=2.718281828459$ 作為目標值。
- 設定累積和 s=0。
- 設定當前項次 n=0
- 設定初始階乘值 factorial=1。
- 計算目標誤差 $ϵ=10^{−t}$。
- 開始累加泰勒展開
- 計算目標誤差 $ϵ=10^{−t}$。使用迴圈,不斷累加公式 $S=S+\frac{1}{n!}$,直到 $\left | e-S \right |<ϵ$ 為止。
如今在電腦領域時代,輸出九宮格並非上面歌訣解法,而是以九宮格走位完成,其規則如下:(可參考 113 年工科技藝競賽第三題:魔方陣)
上面答案與前述九宮歌訣同義,可曰:「九宮之義,法以靈龜,六八為肩,二四為足,左三右七,戴一履九,五居中央。」
現在請你寫一程式,依照上面規則(不是歌訣),輸出魔方陣。
| 演算法 | |
|---|---|
| 簡碼 | 流程圖 |
|
否則: ($row$,$col$) = ($newRow , newCol$) |
 |
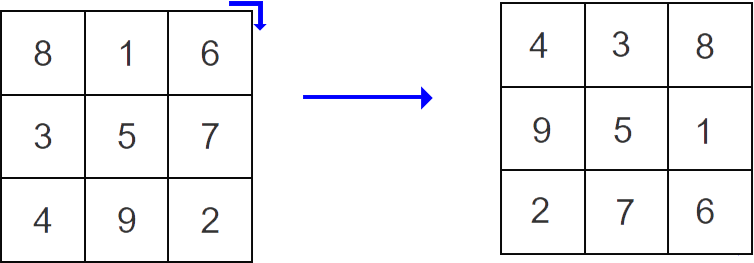 |
| 圖十 |
| 演算法 | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||
| 簡碼 | 流程圖 | ||||||||||||||||||||
|
| |||||||||||||||||||||
它的計算方式可以使用下面泰勒展開式達成。
$e=\sum\limits_{n=0}^{\infty} \frac{1}{n!}=\frac{1}{0!}+ \frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\cdots$
現在假設 $e = 2.718281828459$,請使用迴圈,依照上面公式評估累計到第幾項其誤差會低於 $10^{-t}$。
輸入說明:程式輸入 $t$ ($4\le t\le 12$)。
輸出說明:程式輸出泰勒展開式累計到第幾項時,其值與 $e$ 相差低於 $10^{-t}$。
| 演算法 | |
|---|---|
| 簡碼 | 流程圖 |
|
| |
| 輸入 | 輸出 |
|---|---|
| 4 | 8 |
| 9 | 13 |
| 12 | 15 |