演算法（Algorithm）的定義
演算法是一組明確的指令步驟，用於解決某個問題或完成特定任務。它可以被視為一個步驟式的解法，從輸入到輸出，必須在有限的時間內完成，並且結果是正確且可預測的。

特性
  1. 輸入（Input）：
    2. 演算法接受零個或多個輸入。
    範例：
    做菜需要一些食材及調味料。
  2. 輸出（Output）：
    3. 至少產生一個輸出，通常是解決問題的結果。
    範例：
    最後完成輸出一道菜。
  3. 有限性（Finiteness）：
    4. 演算法必須在有限的步驟內結束，不會無限執行。
    範例：
    不會無止盡一直煮菜。
  4. 確定性（Definiteness）：
    5. 每一步驟必須是清楚的，沒有歧義。
    範例：
    煮菜，不會某個步驟要放糖或是放鹽不清楚。
  5. 有效性（Effectiveness）：
    6. 每一步操作必須可以在有限的時間內完成，並且可以用人類或機器執行。
    範例：
    一道食譜，可以找廚師或煮菜機器人操做。
範例：
  1. 日常生活中的例子：
    • 做菜的食譜就是一種演算法，按順序完成每一步，就能得到一道菜。
  2. 程式設計中的例子：
    • 排序演算法：如冒泡排序（Bubble Sort）、快速排序（Quick Sort）。
    • 搜尋演算法：如線性搜尋（Linear Search）、二分搜尋（Binary Search）。
為什麼需要演算法？
  1. 效率性：
    • 使用高效的演算法可以節省時間與資源。
  2. 普適性：
    • 演算法提供了一種解決問題的通用方式，可以應用於不同的場景。
  3. 可重用性：
    • 一個好的演算法可以在不同問題中重複使用。
簡單範例：
給定一個整數 n，若是質數，則輸出 Yes，否則輸出 No。

先思考再寫步驟。

簡碼
步驟：
  1. 輸入整數 n
  2. 設定旗標 f = false
  3. 設定除數從 2 開始除之。
    1. 若整除，則設定旗標 f=true
  4. 除數加 1，回到步驟 3，直到除數 = n-1。
  5. 如果旗標 f = false，則輸出 Yes 否則輸出 No。
流程圖


程序優化
  1. 找到一個因數就知道非質數，則離開重複計算迴圈。
  2. 搜尋的範圍是否起點為 2，終點為 n-1？
    • 除了 2，所有的偶數均非質數。
      • 所以起點從 3 開始，每次遞增 2。
    • 檢查終點應為  
    		$$int(\sqrt{n})$$
  3. 增強可讀性。
    4. 旗標名稱設定為 prime。

簡碼
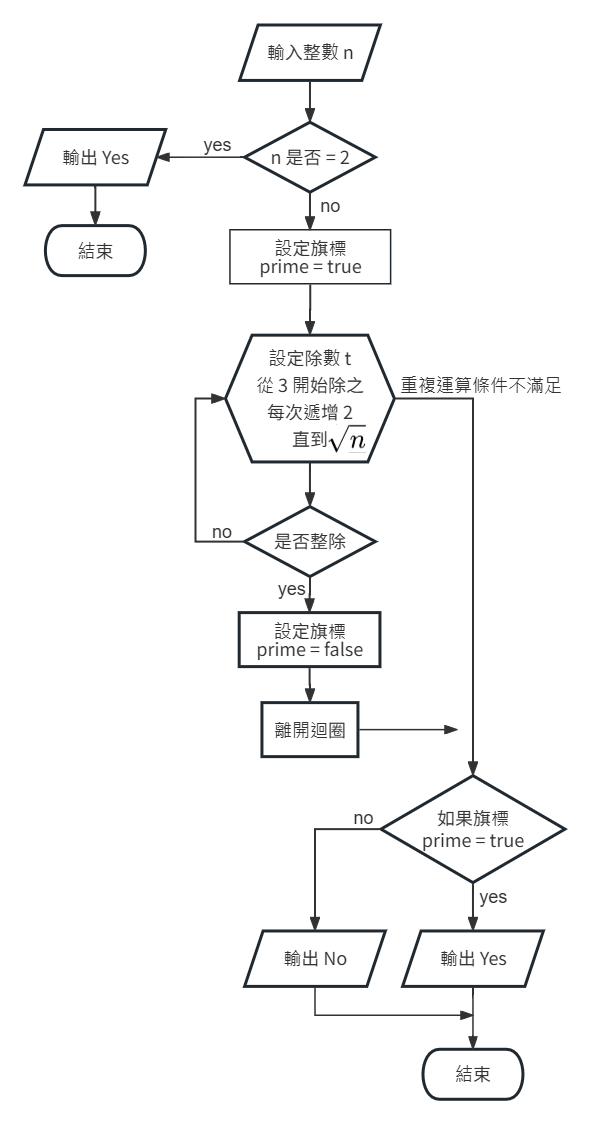
步驟：
  1. 輸入整數 n
  2. 如果 n = 2，則輸出 "Yes"
    3. 否則執行下面程序。
  3. 設定旗標 prime = true
  4. 設定除數從 3 開始除之，每次遞增 2。
    1. 若整除，則設定旗標 prime = false
    2. 離開重複運算迴圈。
  1. 除數加 2，回到步驟 4，直到除數 =  
$$int(\sqrt{n})$$
  1. 如果旗標 prime = true，則輸出 Yes 否則輸出 No。
流程圖